New Radiodont just dropped! it's the tiny Mothra-like Mosura fentoni, you can find out more about it here on this paper: https://royalsocietypublishing.org/doi/10.1098/rsos.242122
I've also got a Patreon now, any support there will help me to keep more videos like this coming in the future. Thanks for watching!
https://www.patreon.com/Kiabugboy
music: https://www.youtube.com/watch?v=x3i7RUQ8Wpk
#paleontology #paleoart #3danimation #anomalocaris #radiodont #cambrianperiod #palaeozoic #blender3d
Richard Elwes explores the world of polyhedra and toroids, including the legendary Holey Monster. More links & stuff in full description below ↓↓↓
Patrons can see an out-take and bonus footage here: https://www.patreon.com/posts/135312036 (or why not become a supporter today and see all our patron-only material)
Stella (the software used): https://www.software3d.com/Stella.php
Richard Elwes at the University of Leeds: https://eps.leeds.ac.uk/maths/staff/4018/dr-richard-elwes-
Or: https://richardelwes.co.uk
His books: https://amzn.to/4fJIhHE
Adventures Among the Toroids was by B.M.Stewart
More on Numberphile...
Goodstein Sequence with RIchard Elwes - https://youtu.be/0Le7NgS-wO0
A new discovery about Dodecaherons - https://youtu.be/G9_l8QASobI
The Tetrahedral Boat - https://youtu.be/-IjGexS1T8U
Paper model & more info about the Webb toroid: https://www.software3d.com/WebbToroid.php
Numberphile is supported by Jane Street. Learn more about them (and exciting career opportunities) at: https://bit.ly/numberphile-janestreet
We are also grateful for support from Ben Delo.
NUMBERPHILE
Website: http://www.numberphile.com/
Video by Brady Haran and Pete McPartlan
Numberphile T-Shirts and Merch: https://teespring.com/stores/numberphile
Brady's videos subreddit: http://www.reddit.com/r/BradyHaran/
Brady's latest videos across all channels: http://www.bradyharanblog.com/
Sign up for (occasional) emails: http://eepurl.com/YdjL9
Brady Haran's lecture at the Royal Society upon receiving the Zeeman Medal... More links & stuff in full description below ↓↓↓
Objectivity Playlist of items featured in the lecture: https://www.youtube.com/playlist?list=PLt5AfwLFPxWLCm7kXoUUjWJ3Ku6uGRBoJ
The 2024 Christopher Zeeman Medal was awarded to Brady Haran in recognition of excellence in the communication of mathematics - https://www.lms.ac.uk/news/brady-haran-2024-christopher-zeeman-medal
It was awarded by the Institute of Mathematics and its Applications and the London Mathematical Society.
Upon receiving the medal, Brady gave this lecture at The Royal Society on May 7, 2025. It was entitled "Treasure Trove: Amazing Objects from the World of Mathematics".
To see the introduction by IMA president elect Heather Tewkesbury, watch here - https://www.youtube.com/watch?v=rlvcRlT_EZA
Thanks to Alex Springer from A Star Studios fro helping out with video footage.
Patreon: http://www.patreon.com/numberphile
Numberphile is supported by Jane Street. Learn more about them (and exciting career opportunities) at: https://bit.ly/numberphile-janestreet
We are also grateful for support from Ben Delo.
NUMBERPHILE
Website: http://www.numberphile.com/
Videos by Brady Haran
Numberphile T-Shirts and Merch: https://teespring.com/stores/numberphile
Brady's videos subreddit: http://www.reddit.com/r/BradyHaran/
Brady's latest videos across all channels: http://www.bradyharanblog.com/
Sign up for (occasional) emails: http://eepurl.com/YdjL9
Try everything Brilliant has to offer for free visiting https://brilliant.org/electroboom. You’ll also get 20% off an annual premium subscription.
Touchscreens are awesome parts of electronics! The new(ish) best way to interact with devices and yet, such simple components.
For Exclusive Content, join:
Patreon: http://patreon.com/electroboom
YouTube membership: https://www.youtube.com/channel/UCJ0-OtVpF0wOKEqT2Z1HEtA/join
Post your submissions to: http://reddit.com/r/electroboom
Instagram: http://instagram.com/mehdi_sadaghdar
TikTok: https://www.tiktok.com/@electroboomguy
Twitter: http://twitter.com/electroboomguy
Facebook: http://www.facebook.com/ElectroBOOM
My articles: https://www.electroboom.com/
Below are my Super HUGE Patrons!
Raphaël (River) Champeimont
Zoddy
Michael Lloyd
My sponsors and top patrons: http://www.electroboom.com/?page_id=727
By: Mehdi Sadaghdar
0:00 Introduction
3:18 Resistive Touchscreen
5:28 Infrared Touchscreen
6:43 Capacitive Touchscreen
When bad news gets me down, I often get insomnia. I wake up in the middle of the night, start thinking about how we’re all doomed, and can’t easily stop. To break out of these doom loops, I do elaborate visualization exercises. They don’t really put me to sleep, they just calm me down. Then later I can fall asleep.
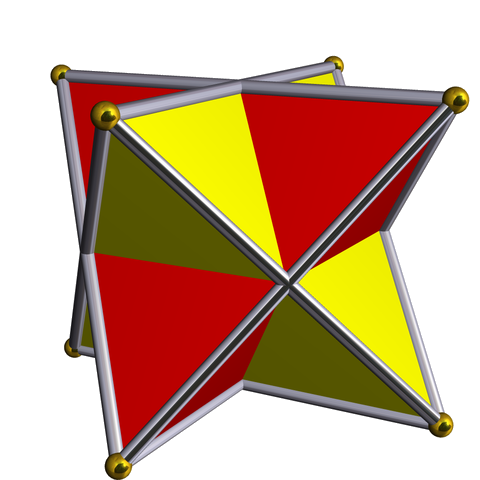
Here’s what I’ve been doing this week. I visualize this shape made of two interpenetrating tetrahedra, called the ‘stella octangula’ or ‘stellated octahedron’. Notice that these two tetrahedra are ‘dual’: each vertex of the yellow one is above the center of a triangle in the red one, and vice versa.
Then I imagine the yellow tetrahedron slowly moving ‘up’ into the 4th dimension while the red one moves ‘down’. At some point, the distance between each corner of the yellow tetrahedron to the 3 nearest corners of the red one equals the distance between any 2 corners of the yellow tetrahedron. Then I’ve got a 4d shape called the ‘cross-polytope’. All its faces are regular tetrahedra.
There are easier ways to think about the cross-polytope, which is one of the six 4-dimensional regular polytopes. So the real challenge is to visualize how this way of getting it leads to the same result.
My go-to way to think about the cross-polytope is to imagine the 4 coordinate axes in 4-dimensional space and put two dots on each axis, one unit away from the origin in each direction:
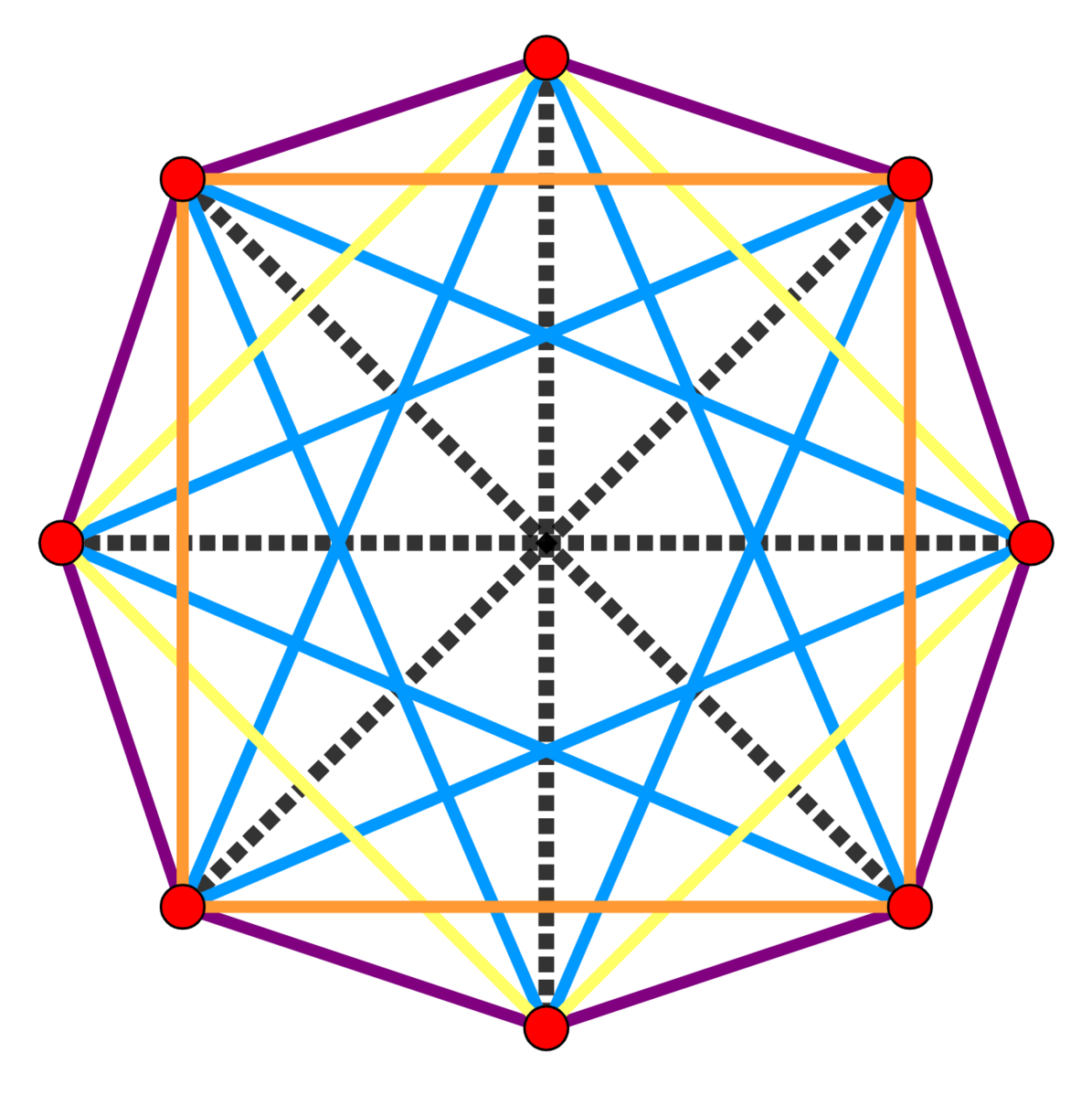
These are the vertices of a cross-polytope. It’s the 4d analogue of an octahedron. Just as the octahedron has equilateral triangles as faces, this guy has regular tetrahedra as faces. Can you see what they are, and count them?
Don’t worry—if you’re too busy now, you can do it when you’re lying in bed at 3 am thinking about global warming and the decline of democracy. Start by visualizing this picture:
Then visualize the tetrahedra. But the hard part is to rotate this cross-polytope in your mind so you see it as made of two dual tetrahedra, one red and one yellow, and an edge connecting each vertex of the red one to the 3 nearest vertices of the yellow one. That’s been keeping me busy every night this week.
By the way, everything I just said has a 3d version! The 3d analogue of the cross-polytope is a regular octahedron. The corners of a regular octahedron are
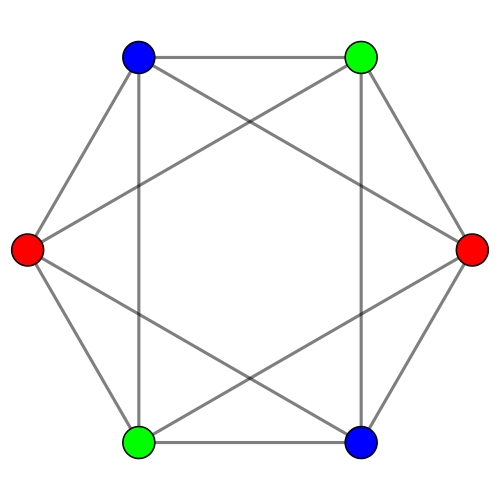
But here’s a flattened picture of an octahedron:
See the two interpenetrating equilateral triangles? If you move one up, and move one down, they can become two opposite faces of a regular octahedron.
Actually this sort of trick works in any dimension. Take two regular n-simplexes, dual to each other and interpenetrating; then move one ‘up’ into the (n+1)st dimension and the other ‘down’. At some point their vertices will be the vertices of an (n+1)-dimensional cross-polytope. In 3 dimensions this is easy for me to visualize, while in 4 dimensions I can just barely visualize it… though it’s getting easier every night.
Log in
reply
